
FACTORIZACIÓN
En matemáticas, la factorización es una técnica que consiste en la descomposición de una expresión matemática (que puede ser un número o una suma). Antes que todo, hay que decir que todo polinomio se puede factorizar utilizando números reales, si se consideran los números complejos. Existen métodos de factorización para algunos casos especiales, que son:
- Diferencia de cuadrados
- Suma o diferencia de cubos.
- Suma o diferencia de potencias impares iguales.
- Trinomio cuadrado perfecto.
- Trinomio de la forma x²+bx+c
- Trinomio de la forma ax²+bx+c.
- Factor común.
DIFERENCIA DE CUADRADOS
La diferencia de cuadrados es una
práctica que necesitamos tener clara para seguir avanzando en nuestro curso de
Álgebra. Lo primero de todo es entender el concepto, saber qué significa la
diferencia de cuadrados y cómo podemos ponerla en práctica. Por lo tanto,
empecemos por el principio, la definición de diferencia de cuadrados.
Se le llama diferencia de cuadrados al binomio conformado por dos términos a
los que se les puede sacar raíz cuadrada exacta.
Al estudiar los productos notables teníamos que:

En donde el resultado es una diferencia de cuadrados, para este capítulo es el caso contrario:

Donde siempre la diferencia de cuadrados es igual al producto de la suma por la diferencia de sus bases.
Pasos a seguir para calcula la diferencia de cuadrados:
- Se extrae la raíz cuadrada de ambos términos.
- Se multiplica la suma por la diferencia de estas cantidades (el segundo termino del binomio negativo es la raíz del termino del binomio que es negativo)
Factorización de una diferencia de cuadrados
La factorización de una diferencia de cuadrados está formada por una ecuación con dos términos: uno positivo y el otro, negativo. Ambos deben de ser raíces cuadradas exactas. Y lo que se hace es realizar una resta entre ellos. De ahí el nombre de factorización por diferencia de cuadrados

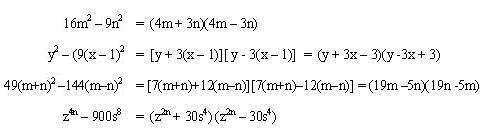
Recuerda que tanto la diferencia de cuadrados como la factorización por diferencia de cuadrados te serán de gran utilidad para resolver problemas matemáticos y de álgebra en concreto. ¡No pases a la siguiente lección hasta que tengas claro este concepto! Solo así podrás ir aprendiendo paso a paso.
Suma o diferencia de cubos.
La suma o diferencia de dos cubos puede factorizarse en un producto de un binomio por un trinomio.
La suma de dos cubos perfectos se descompone en dos factores:
- La suma de sus raíces cúbicas.
- El cuadrado de la primera raíz, menos el producto de las dos raíces, más el cuadrado de la segunda raíz
a^3 + b^3
- Raíz cúbica del primer término a^3 es a
- Raíz cúbica del primer término b^3 es b
a^3 + b^3 = (a + b)(a^2 - ab + b^2)
La diferencia de dos cubos perfectos se descompone en dos factores:
- La diferencia de sus raíces cúbicas.
- El cuadrado de la primera raíz, más el producto de las dos raíces, más el cuadrado de la segunda raíz
a^3 - b^3
- Raíz cúbica del primer término a^3 es a
- Raíz cúbica del primer término b^3 es b
a^3 - b^3 = (a - b)(a^2 + ab + b^2)
Suma o diferencia de potencias impares iguales.

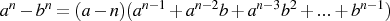
En este caso solo aplica para potencias impares iguales, porque para las potencias pares iguales se puede factorizar por suma o diferencia de cuadrados
Se debe tener en cuenta que ambos términos estén elevados a una potencia impar mayor o igual que "5". Este proceso también demuestra la suma y diferencia de cubos, ya que "3" es un número impar.
Trinomio cuadrado perfecto
Un trinomio cuadrado perfecto, por brevedad TCP, es un polinomio de tres términos (también llamado trinomio) que resulta de elevar al cuadrado un binomio.

Trinomio de la forma x²+bx+c
X² + 5x + 6, a²
- 2 a - 15, m²
+ 5m -14, y²
- 8y +15
Regla para factorizar un trinomio de la forma x²+bx+c
1) El trinomio se descompone en dos factores binomios cuyo primer término sea la raíz cuadrada del primer término del trinomio.
2) Se buscan dos números que sumados algebraicamente den como resultado el coeficiente del segundo término b, y multiplicados den el tercer término c.

Trinomio de la forma ax²+bx+c
ste tipo de trinomio se diferencia del anterior debido a que el termino al cuadrado () se encuentra precedido por un coeficiente diferente de uno (debe ser positivo). Este se trabaja de una manera un poco diferente, la cual detallamos a continuación:
- Multiplicamos el coeficiente "a" de el factor "a" por cada termino del trinomio, dejando esta multiplicación indicada en el termino "bx" de la manera "b(ax)", y en el termino "a" de la manera .
- Se descompone el trinomio en dos factores binomios cuyo primer termino será la raíz cuadrada del termino la que seria "ax".
- al producto resultante lo dividimos entre el factor "a", con el fin de no variar el valor del polinomio.
- El signo del primer binomio será el mismo signo que tenga el termino "bx", el signo del segundo binomio será igual a la multiplicación de los signos de "bx" y de "c".
- Se buscaran los segundos términos de los binomios según los pasos tres y cuatro del caso del trinomio anterior.

Factor común

Se dice que un polinomio tiene factor común cuando una misma cantidad, ya sea número o letra, se encuentra en todos los términos del polinomio.
Si en todos los términos de un polinomio figura un factor común, dicho polinomio es igual al producto de ese factor por el polinomio que resulta al dividir cada término por ese factor.
Para efectuar el factor común hay que tomar en cuenta que este se realiza tanto para los números como para las letras, y con las letras se toma la que tenga el menor exponente de todas.